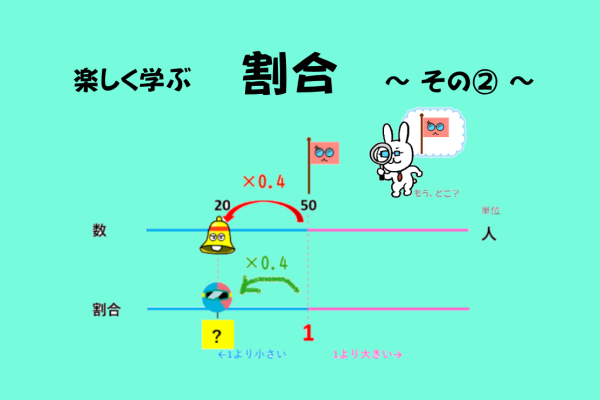
『割合』は、小学5年生・算数の中で苦手意識を感じている子供がとても多い分野です。
この割合について、苦手な子供でもわかりやすいようにイラストや図を使いながら楽しく学習する方法をお伝えしていきます。
苦手克服のための練習用紙を無料でダウンロードすることができますので、ご活用ください。
例えば、半分を割合で表す方法は、いくつかあります。
小数で表すと・・・ 0.5
百分率で表すと・・・ 50%
分数だで表すと・・・ 1/2
今回は、このうち小数で表される割合について詳しく解説していきます。
ステップバイステップで段階的に学習するために、何回かに分けて記事を更新していきます。
今回は第二弾、『割合(小数)・その②「割合」と「もとにする量」を求めよう!』です。
1章:前回(その①)までの復習
割合とは
(今回は、割合の中でも小数のみを扱います。)
ある基準を決めて、それを1とした時、どのくらいの部分をしめるかを小数で表したものです。
割合は、○○倍という言葉でイメージしておくとわかりやすいと思います。
①もとにする量
基準となる数のことです。

もとにする量 → もとにい
②割合
もとにする量(基準の量)を1とした時、どのくらいの部分を占めるか小数で表したもの。

わりあい → わりあい マン
③比べる量
もとにする量に割合をかけた量。
つまり、
もとにする量 × 割合 = 比べる量

くらべる量 → くらべる くん
※小学生の息子作:はちまきを巻いて、いつも「比べるぞ~」と気合が入っているそうです。

もしもわからなかったら、その①の記事にもどって学習してみてくださいね。


割合の練習用に数直線のシートを作りました。
必要な方は、下記ボタンからファイル(PDF)をダウンロード(無料)して使ってみてください。
2章:『割合』(小数)を求めよう!~練習問題あり
まず前回に学習した『比べる量を求める式』を使って、この式から『割合』を求めてみましょう。

※『比べる量』の式がわからなければ、その①の記事を読んでくださいね。
『割合を求める式』じゃないのに使えないよ!と思った方、

かんたんなので、大丈夫!
ゆっくり説明していきます。
かけ算と割り算の行ったり来たりに慣れよう!
まず、割合の学習の前に知っておきたい算数の基そ知識について説明します。
それは、『かけ算と割り算の関係』です。
これが使いこなせると今後便利なので、かんたんな例題を使って説明していきます。
◆◆◆例題①◆◆◆

20の2倍は40ですよね。
20×2=40
↓

じゃあ、40を20にもどす時はどうしたらいいかな?
×2する前にもどしたいのだから、÷2をすればもどりますよね。

絵にしたらこんな感じになります!

では、もう1問だけ。
◆◆◆例題②◆◆◆

20の0.9倍は18ですよね。
20×0.9=18
↓

じゃあ、18を20にもどす時はどうしたらいいかな?
×0.9する前に、もどしたいのだから、÷0.9をすればもどりますよね。

【まとめ】

ある数字をかけたら、同じ数字で割ればもとにもどる。
↓
逆に、ある数字で割ったら、同じ数字をかければもとにもどる。
かけ算と割り算の行ったり来たりをマスターしましょう!
(当たり前と言えば当たり前・・・。)
『割合』(小数)を求める式を考えよう!
じゃあ、『割合』の話にもどって考えてみましょう!

この式をもとに、『割合』を求めてみます。
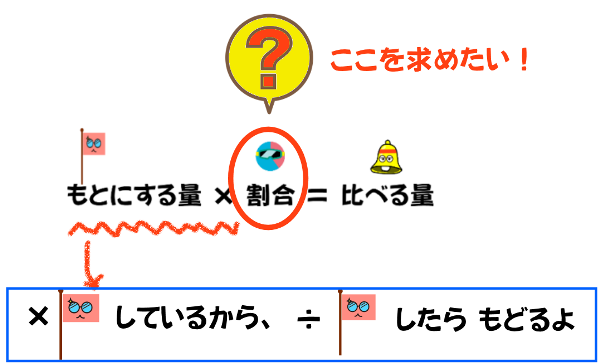
つまり、次のようになります。
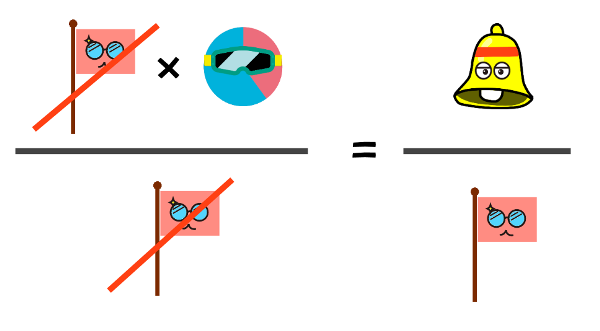
『割合』を求める式の完成!
このように考えたら、自分で割合の式を導けますよね。

ちょっと難しいという方は・・・


練習問題では、数直線を使った方法で解説していきます。
どちらの方法が自分に合っているか考えてみてくださいね。

- 解き方①
『比べる量を求める式』、『割合を求める式』、『もとにする量を求める式』の3式のうち、どれか一つ覚えていれば自分で導くことができます。あなたが一番覚えやすい式は、どの式かな?
- 解き方②←練習問題はこちらで!
数直線を使って解くこともできます。
では、いよいよ練習問題を解いて確認していきましょう!
今回は数直線を使って解く方法をお伝えします。
◆練習問題①~割合を求めよう!
りんごが10個あります。りんごの個数を割合1としてメロン5個の割合を小数で求めましょう。
まず、やることは『もとにする量』をつきとめることです。
文章中では、例えば、
- ~の数の○○倍
- ~の数をもとにすると
- 全体の○○倍
- ~の数を1とすると
など、様々な表現になって登場しますよ。
わかりにくく文章中にまぎれこんでいるのです!?

『りんごの個数を割合1として』という文章から、りんごの個数が『もとにする量』だと気が付きましたか?
(わからない場合は、あせらずにその①の記事にもどってみてね。)
数直線を書いて頭を整理してみましょう!
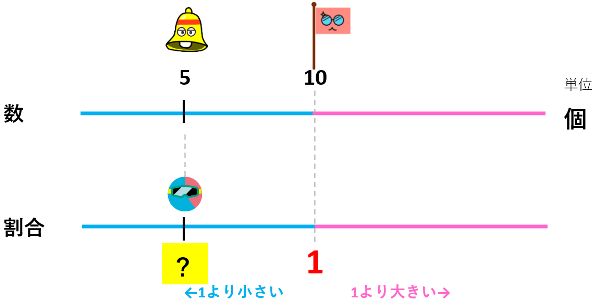
次は、メロンの5個が『もとにする量』の何倍なのか見てみましょう。
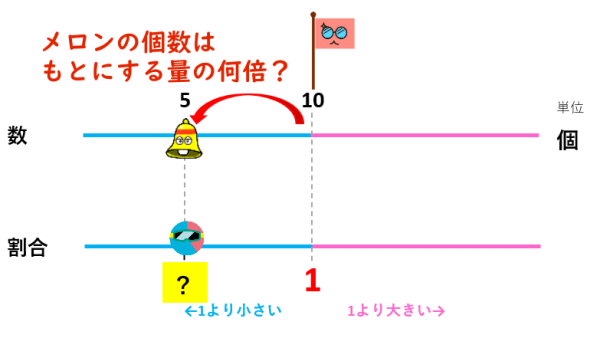
5÷10=0.5で、0.5倍ですよね。
数(量)が0.5倍になら、割合も0.5倍になります。
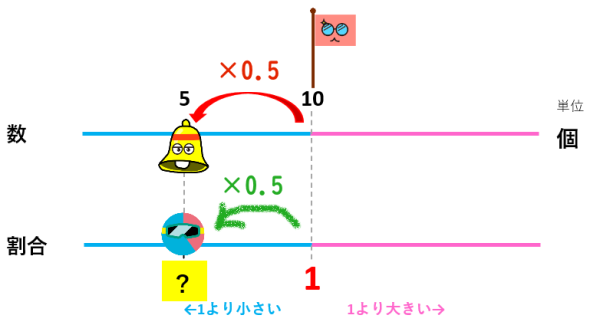
だから、
メロンの5個の割合は0.5が答えになりますよ。
数直線で『割合』を求めても、

になりましたね。
もう1問だけ練習しておきましょう。
◆練習問題②~割合を求めよう!
校庭に生徒が50人います。そのうち20人は女の子です。女の子の人数は全体の何倍ですか。
手順は練習問題①と一緒です!
また、『もとにする量』をつきとめることからです。

『全体の何倍』という文章から、全体の人数が『もとにする量』だと気が付きましたか?
(わからない場合は、あせらずにその①の記事にもどってみてね。)
数直線を書いてみると頭が整理されますよ。
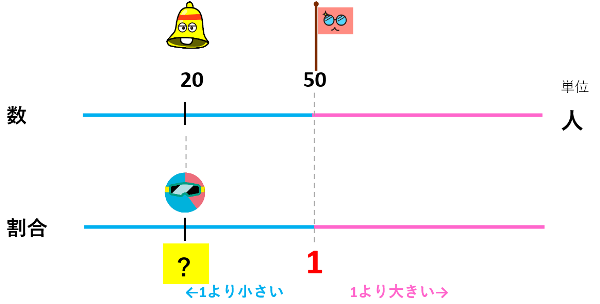
次は、女の子の人数が『もとにする量』の何倍なのか見てみましょう。
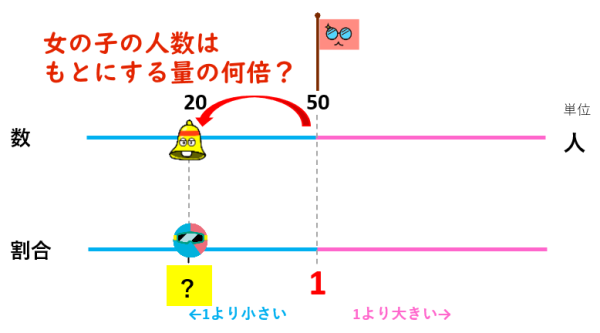
20÷50=0.4で、0.4倍ですよね。
数(量)が0.4倍なら、割合も0.4倍になります。
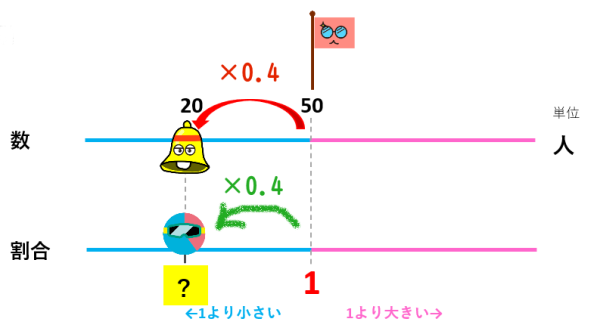
だから女の子の人数は全体の0.4倍が答えになります。
数直線で『割合』を求めても、

になりましたよね。
【参考資料】~何倍なのか求められますか?~
例)4は2の何倍ですか。
これなら感覚的に2倍だとすぐわかりますよね。
これは、『求めたい数字』÷『もとの数字』の計算をしているのです。
だから、4÷2=2で2倍になるんですね。
例)2は4の何倍ですか。
『求めたい数字』÷『もとの数字』で同様に求めることができるので、
2÷4=0.5で0.5倍となります。
3章:もとにする量を求めよう!~練習問題あり
今回は、『もとにする量』を数直線を用いて求めてみましょう。
◆練習問題①~もとにする量を求めよう!
りんごが30個あります。りんごの個数が1.5の割合になるとすると、割合1にあたるメロンの個数はいくつですか。
ちょっとややこしい文章ですが、一つ一つ見ていきましょう!
また、『もとにする量』をつきとめることからです。

『割合1にあたるメロンの個数』という文章から、メロンの個数が『もとにする量』だと気付きましたか?
(わからない場合は、あせらずにその①の記事にもどってみてね。)
数直線を書いてみると頭が整理されますよ。
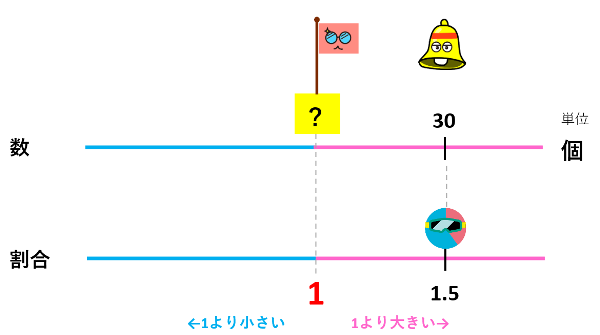
数直線を見ると、りんごの割合がメロンの割合の1.5倍になっていることがわかりますよね。
割合が1.5倍になるということは、数(量)も1.5倍になるはずです。
でも、今求めたいのは1.5倍する前のメロンの個数?ですよね。
1.5倍する前にもどすには1.5で割ることを覚えていますか?
(わからない場合は、2章を見てね。)
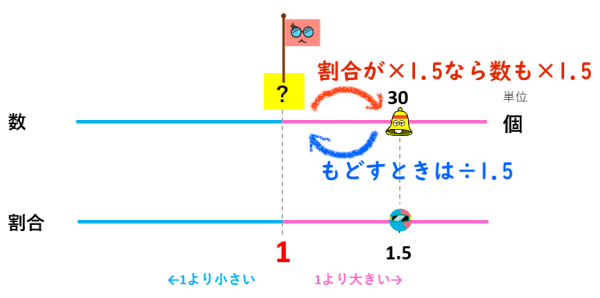
だから、
?(もとにする量)=30(比べる量)÷1.5(割合)=20
となり、メロンの個数は20個になります。
『もとにする量』を式にすると次のようになりますよ。


覚えられる子は式を覚えてもOK!
覚えられなかったら自分で式を導けば大丈夫!
自分に合ったやり方を見つけましょう。
4章:算数が苦手な子供への具体的な対処法
苦手分野が何かと多い小学生の息子と家庭学習する中で、私が必要だと感じた対処法は次の通りです。
算数が苦手な子供への具体的な対処法
- ステップ バイ ステップで!
確認とまとめを繰り返しながら、少しずつ教える。
- イラストや色の活用
覚えにくいことはイラストに置き換えてみたり、赤や青など2~3色の色を使って色分けしながら教える。
- ある程度の『型』を覚える
丸暗記にならないよう、ちゃんと意味も考えさせるように工夫する。
- 算数嫌いにならない工夫
子供の好みに合わせて、楽しませる工夫をする。
我が家の例)
ばかばかしくて笑えることが好きな息子と、算数のオリジナルキャラクターを考える。
【参考情報】
『すらら』という通信教材は、算数の苦手克服にとても適していると思います。我が子の反応などは無料体験記事を参考になさってください。

※無料体験の中に『割合』の単元は無かったと思いますが、無学年式なので何年生の単元でも体験することができます。