例えば、473÷52という割り算の筆算をする時に、なかなか『商』が見つからないという悩みはないでしょうか。
この記事では、割り算の筆算の『商』の探し方のコツをお伝えしています。練習問題もダウンロードすることができるので、苦手克服などに是非活用してみてください。
ここでご紹介している方法は、実際に割り算の筆算に苦労していた我が子の為に考えたものです。同じように苦手意識のあるお子様は参考になさってください。
ちゃんと考えている?~筆算の意味
小学4年生になり、学校で「分配の法則」について習ったそうです。
その時息子が言ったことは、

ぼく、分配の法則なんて初めてだからわからないよ。
覚えろというなら覚えるけど、本当は覚えたくないな。必要なの?
という内容でした。
そこで、
本当に初めてかな?
知らず知らずのうちに使っていないかな??
という点から考えてみました。

それを考えるために、まず「かけ算の筆算」から始めましょう!
67×4を例にとって、筆算について考えてみます。
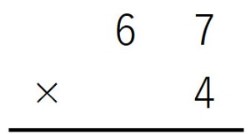
4×7=28→2くり上がって→4×6=24を桁をずらして書いて→・・・


きっと、学校で習った方法で解けると思います。
では、どうして緑枠のように書くのかを、きちんと考えたことはありますか?
実は、こういうことをしているのです↓
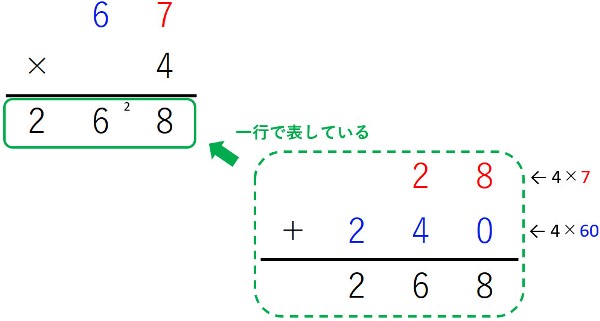
点線ので囲まれた部分を一行で書き表しているのです。
67とは、十の位の6が60を一の位の7が7を表しているので、(60+7)と考えることができますよね。
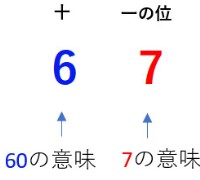
だから、67×7を式で表すと次のようになります。

これが、「かけ算の筆算の正体」です!

何も考えないで解くと、分配の法則が隠れているようには見えませんが、「実はいつも分配の法則を使っていた!」ということになります。

5×12を暗算する時に、5×10と5×2で別々に計算して、後で足し合わせて求めたりすることも同様です。実は、意外と便利に日常の中で使っているのが、分配の法則なのです。
そう考えれば、少し苦手意識が薄れませんか?
「分配の法則」とは
ここで、分配の法則について、一度まとめておきましょう。
【分配の法則】
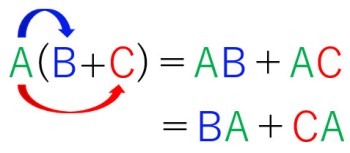
()の後ろにAがきても同じです。

67×4を例にとると、
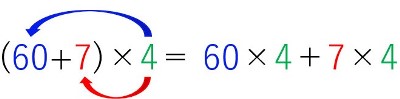
となりますね。
【関連記事】

基本編:「分配の法則」を割り算の筆算で使ってみよう!
【例1】473÷52
百の位と十の位の商は立たないので、一の位に立てる商を探します。
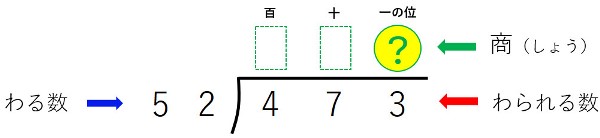
割る数×商を割られる数に近づければよいので、

となります。
ここで、
商に当たりをつける時に、まず割る数「52」に注目してみましょう。
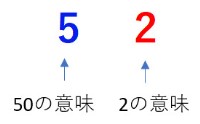
52は50+2となります。
つまり、

ことになりますね。
分配の法則を使って表すと、
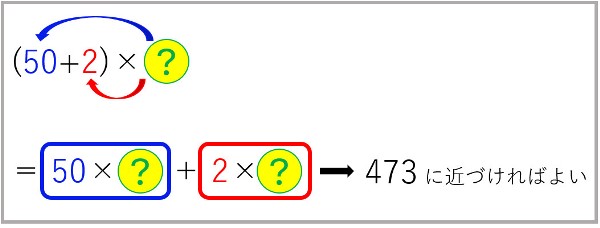
青枠と赤枠の項の大きさを比べた時、必ず、


このようにすれば、
割る数「52」の50の部分にだけ着目して、商に当たりをつけることができます。
50×?を473に近づけるには、50×9=450とすればよいので、?を9と考えて検算をしてみましょう。
(50+2)×9=50×9+2×9=450+18=468 ≦ 473 ・・・OK
473以下なので、?は9で成立します。
だから、答えはこうなります。
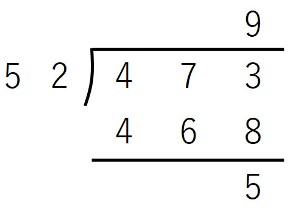
【例2】145÷39
百の位と十の位の商は立たないので、一の位に立てる商を探します。
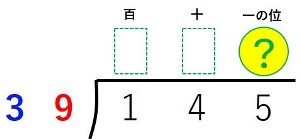
割る数×商を割られる数に近づければよいので、

となります。
分配の法則を使って表すと、
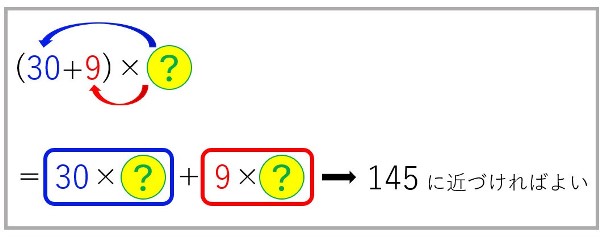
青枠と赤枠の項の大きさを比べた時、必ず、


このようにすれば、
割る数「39」の30の部分にだけ着目して、商に当たりをつけることができます。
30×?を145に近づけるには、39×4=120とすればよいので、?を4と考えて検算をしてみましょう。
(30+9)×4=30×4+9×4=120+36=156 > 145 ・・・NG

検算すると
(30+9)×3=30×3+9×3=90+27=117 ≦ 145 ・・・OK
145以下なので、?は3で成立します。
だから、答えはこうなります。

【解き方のまとめ】
- ステップ1
割る数の桁の大きい方をもとにして、商に当たりをつける。
- ステップ2
当たりをつけた商が正しいか検算をする。
- ステップ3
正しくなければ数字を小さくして、成り立つ数字を探す。

ステップ3で、どれくらい数字を小さくするかについては、子どもの判断に任せています。難しい場合には、1ずつ減らすことから始めてみてください。
練習問題(pdfファイル)は、緑ボタンよりダウンロード可能です。
基本が出来たら徐々に暗算を
慣れてくると、頭の中で少し暗算をしてから商の当たりをつけられるようになってくると思います。
息子の様子から、具体例を2つあげてみます。
【例1】123÷19
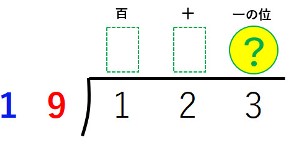
割る数×商を割られる数に近づければよいので、

となります。
分配の法則を使って表すと、


今まで説明してきた手順通りに行けば青枠だけを先に考えますが、
慣れてきたら、頭の中で青枠と赤枠を暗算して・・・
10×9+9×9=90+81=171
暗算してみたら、細かい計算をしなくてもすぐ123を超えることが分かったので、

このように、考えられると更に計算が速くなります。
→8→7→6
とする子もいれば、8を飛ばして、
→7 →6
としたり、
一気に正解の商を導く子もいるかもしれません。あとは練習を積んで感覚をみがいていきましょう!
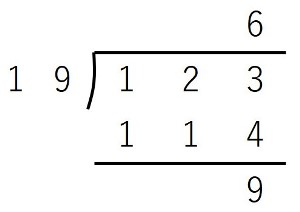
【例2】120÷26
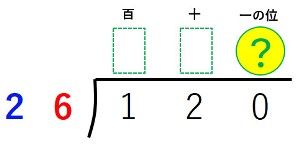
分配の法則を使って表すと、
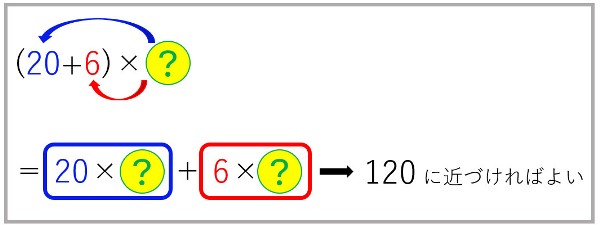
20×6+6×6=120+36=156
暗算してみたら、そもそも青枠だけで120になるので、絶対に120を超えるとわかります。

このように、考えられると更に計算が速くなります。
→5→4
とするか、一気に4まで小さくしてみましょう。
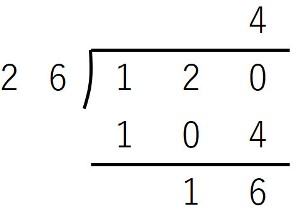
練習問題(商が2桁の問題)

商が2桁でも、解き方は同じです。
3桁÷2桁(あまり有り)で、練習問題を解いてみましょう!
練習問題(pdfファイル)は、緑ボタンよりダウンロード可能です。