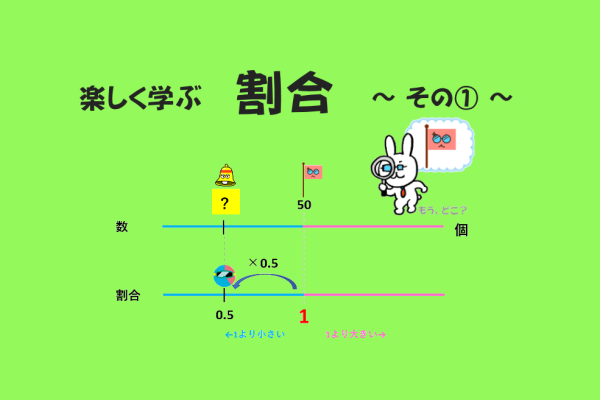
『割合』は、小学5年生・算数の中で苦手意識を感じている子供がとても多い分野です。
この割合について、苦手な子供もわかりやすいようにイラストや図を使いながら楽しく学習する方法をお伝えしていきます。
苦手克服のための練習用紙を無料でダウンロードすることができますので、ご活用ください。
例えば、半分を割合で表す方法は、いくつかあります。
小数で表すと・・・ 0.5
百分率で表すと・・・ 50%
分数だで表すと・・・ 1/2
今回は、このうち小数で表される割合について詳しく解説していきます。
ステップバイステップで段階的に学習するために、何回かに分けて記事を更新していきます。
今回は第一弾、『割合(小数)・その①比べる量を求めよう!』です。
1章:『割合』とは何だろう?(小数編)
割合とは
(今回は、割合の中でも小数のみを扱います。)
ある基準を決めて、それを1とした時、どのくらいの部分をしめるかを小数で表したものです。
割合は、○○倍という言葉でイメージしておくとわかりやすいと思います。

基準を何に決めるのかは問題によって変わるので、文章題の場合には基準が何かを見極めることが大切になります。
では、具体例をあげながら『割合(小数)』について、もっと詳しくみていきましょう。
※この記事の中に出てくる割合とは、小数で表す割合のことを意味しています。
◆具体例①
50個のりんごの2倍は何個ですか。

割合の問題は、数直線を2本書くとわかりやすいですよ!
くわしく説明しましょう。
『個数の数直線』と『割合の数直線』の2本を使います。

まず、問題の「50個のりんごの2倍」という文章から、50個のりんごを基準にすることがわかりましたか?
割合は、基準にするものを1と考えます。
だから次図のような数直線を2本書いてみましょう。
りんご50個という個数が、割合1となります。
この2倍なので、割合1に2をかけて、割合は2になりますよね。
割合が2倍になれば、個数も2倍になりますので、
50個×2=100個 が答えになります。

さて、ちょっとだけややこしい話ですが、上図の①、②、③にはそれぞれに名前があります。
名前を覚えることよりも、それぞれの意味を考えることが大切なので、名前が覚えられない場合にはマークやイラストにするなど工夫してみましょう。
今回は、名前を覚える一例として、小学生の息子と一緒に①~③のキャラクターマークを考えてみました。
①もとにする量
基準となる数量のことです。

もとにする量 → もとにい
②割合
もとにする量(基準の量)を1とした時、どのくらいの部分を占めるか小数で表したもの。

わりあい → わりあい マン
③比べる量
もとにする量に割合をかけた量。
つまり、
もとにする量 × 割合 = 比べる量

くらべる量 → くらべる くん
※小学生の息子作:はちまきを巻いて、いつも「比べるぞ~」と気合が入っているそうです。
もう一つ例をあげてみますね。
意味を確認しながら解いてみてください。
◆具体例②
50個のりんごの0.5倍は、何個ですか。

まず、問題の「50個のりんごの0.5倍」という文章から、50個のりんごが『もとにする量』だとわかりましたか?
もとにする量の割合は1と考えまよね。
だから次図のような数直線を2本書いて考えてみましょう。
上:数量で表した数直線
下:割合で表した数直線
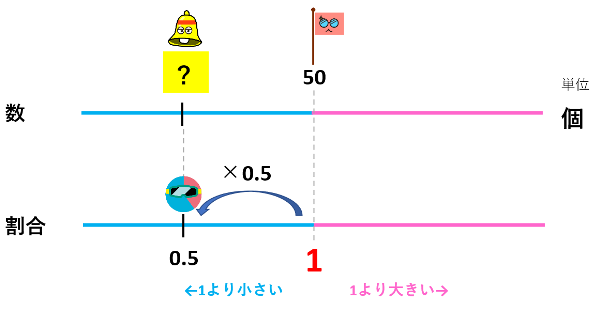
りんご50個という個数が『もとにする量』なので、もとにする量を割合で表すと1となります。
↓
今求めたい「50個のりんごの0.5倍のりんごの個数」が『比べる量』になりますよ。個数がわからないので?にしておきましょう。
↓
比べる量の割合は、もとにする量の割合に対して0.5倍です。
だから、割合1に0.5をかけて、比べる量の割合は0.5になりますよね。
↓
割合が0.5倍になれば、個数も0.5倍になりますので、
50個×0.5=25個 が答えになります。

- もとにする量の割合は1である。
- 比べる量の割合は、1より大きいことも1より小さいこともある。

割合の練習用に数直線のシートを作りました。
必要な方は、下記ボタンからファイル(PDF)をダウンロード(無料)して使ってみてください。
2章:『比べる量』を求めよう!~練習問題あり
文章題から情報を読み取る練習をしていきましょう。
まずは、1つだけ復習をしますね。

練習問題で説明していきますので、頑張って覚えていきましょう!
(勝手に金の公式と名付けました。)
◆練習問題①~比べる量を求めよう!
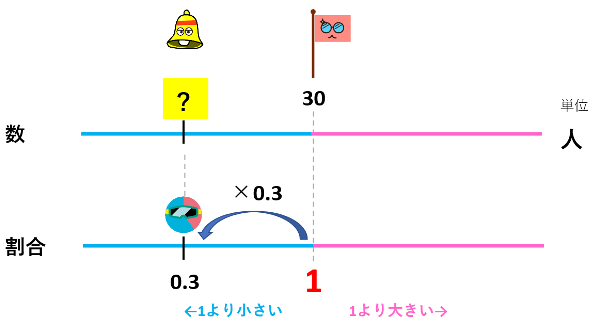
1組は30人の生徒がいます。今日はクラス全体の0.3倍の人がお休みしました。今日お休みした人数は何人ですか。
まず、やることは『もとにする量』をつきとめることです。
文章中では、例えば、
- ~の数の○○倍
- ~の数をもとにすると
- 全体の○○倍
- ~の数を1とすると
など、様々な表現になって登場しますよ。

今回の問題だと、『クラス全体の0.3倍』という文から、クラス全体の人数が『もとにする量』なのだと気が付くことがスタート地点です。
(わからない場合は、あせらずに1章にもどってみてね。)
それがわかったら、数直線にしてみましょう!
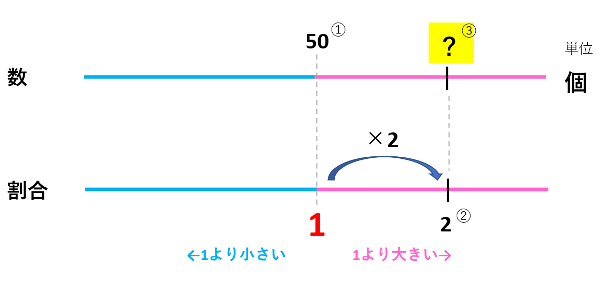
【数直線を書くヒント】
クラス全体の人数30人が『もとにする量』なので、割合1となります。
↓
今求めたいものは、お休みした人の人数ですよね。
これが『比べる量』になりますよ。まだ人数はわからないので?としておきましょう。
↓
お休みした人数は『もとにする量の割合1』に対して0.3倍です。
だから、割合1に0.3をかければ、お休みした人の割合が0.3とわかります。
↓
割合が0.3倍になれば、個数も0.3倍になりますので、
30人×0.3=9人 が答えになります。
求めたかったものは、『クラス全体の0.3倍の人数』です。だから、割合ではなく数量(人数)で答えますよ。
今求めた答えが、『比べる量』と呼ばれるものです。


くり返し練習をして、数直線を書かなくても直にこの式から求められるようになったら、もっとすごいですね!
自分のペースであせらず一歩ずつ進んでくださいね。
もう1問!
◆練習問題②~比べる量を求めよう!
りんごが50個あります。りんご50個を1として、0.8の割合のりんごの個数を求めましょう。
また、これです。

『もとにする量』が何かつきとめます。
『りんご50個を1として』という文章から、りんご50個が『もとにする量』だとわかります。
(わからない場合は、あせらずに1章にもどってみてね。)
これを2つの数直線にしてみましょう!
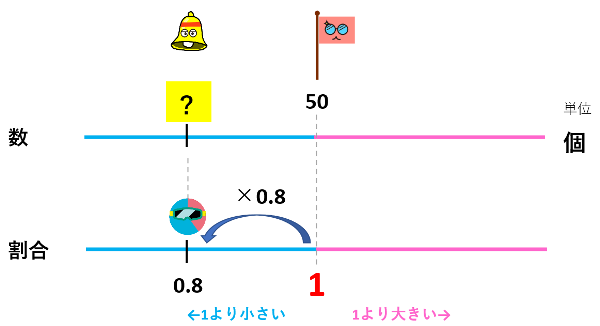
ここまで書けてしまったら、練習問題①と同じ解き方です。

50個×0.8=40個 が答えになります。
最後にもう一問だけ!
◆練習問題③~比べる量を求めよう!
ゆきさんはリボンを10m持っています。りかさんはゆきさんの1.3倍のリボンを持っています。りかさんのリボンの長さは何mですか。
何度でも登場!
またまた、これです。

『もとにする量』が何かつきとめます。
『ゆきさんの1.3倍の』という文章から、ゆきさんのリボンの長さが『もとにする量』だとわかります。
(わからない場合は、あせらずに1章にもどってみてね。)
これを2つの数直線にしてみましょう!
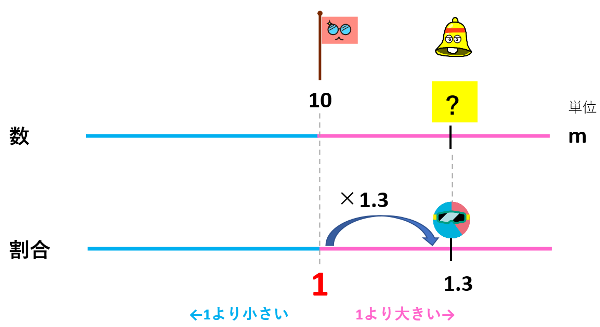
ここまで書けてしまったら、練習問題①と同じ解き方です。

10m×1.3=13m が答えになります。
【まとめ】

- 『もとにする量』が何かつきとめよう!
- 2本の数直線を書くとわかりやすい!
- なれてきたら、下の式から求めてみよう!


たくさんむずかしいことを覚えたので、今回はここまで。
次回その②では、『割合を求める練習』と『もとにする量を求める練習』をします。
今回の内容を理解していることがとても大切になってきますので、何回も練習してみてくださいね!
5章:算数が苦手な子供への具体的な対処法
苦手分野が何かと多い小学生の息子と家庭学習する中で、私が必要だと感じた対処法は次の通りです。
算数が苦手な子供への具体的な対処法
- ステップ バイ ステップで!
確認とまとめを繰り返しながら、少しずつ教える。
- イラストや色の活用
覚えにくいことはイラストに置き換えてみたり、赤や青など2~3色の色を使って色分けしながら教える。
- ある程度の『型』を覚える
丸暗記にならないよう、ちゃんと意味も考えさせるように工夫する。
- 算数嫌いにならない工夫
子供の好みに合わせて、楽しませる工夫をする。
我が家の例)
ばかばかしくて笑えることが好きな息子と、算数のオリジナルキャラクターを考える。
【参考情報】
『すらら』という通信教材は、算数の苦手克服にとても適していると思います。我が子の反応などは無料体験記事を参考になさってください。

※無料体験の中に『割合』の単元は無かったと思いますが、無学年式なので何年生の単元でも体験することができます。