この記事では、立体図形の骨組みをしゃぼん玉液に入れた時に、図形の内側にできる泡の膜同士が120°で交わる不思議に着目し、『科学の視点でものごとを観察する楽しさ』についてお伝えしています。
子供たちにとって、科学現象の原理、特に目に見えない原子や分子などの世界を理解することは、とても難しいことです。
だからこそ、まずは身の回りにある科学の不思議にたくさん触れて、「楽しいな、ふしぎだな」と親しんでおくことが科学好きへの第一歩ではないかと感じます。
自身も科学系の教員を親に持ち、何気なく部屋に置いてあった実験器具をいたずらしながら幼少期を過ごし、気付けば科学好きになっていました。
「なぜ?ふしぎ!」
そんな小さな感動から、科学や数学(算数)を好きになってくれる子供が一人でも増えてくれたらとても嬉しいです。
科学実験~しゃぼん玉の泡のふしぎを見つけよう!
【準備するもの】
- 立体図形を作る針金・ストロー・モールなどの材料
※立体図形の作り方は後ほど解説 - 深めの容器(しゃぼん玉液を入れる)
- 液体洗剤と水
【立体図形の作り方】
針金などで成形できる方は、針金だけで作ってみてください。
私は、針金だと難しかったので、「ストローとモールでつくる幾何学オブジェ」という本を参考にして立体図形を作りました。
私が作った立体図形はこちらです。
しゃぼん玉液に完全につかるように、容器のサイズに合わせて一辺の長さを決めてください。

今回は、正六面体と、正四面体のみを作成しましたが、例えば三角柱や正八面体など他にも色々な立体図形で実験することが可能です。(上記の本にも作り方が掲載されています。)
作りやすい方法でお好みの立体図形を作ってみてください。
【しゃぼん玉液の作り方】

500mlの水に対して、液体洗剤50ml入れて静かにかき混ぜます。
※もう少し濃度を薄くしてもしゃぼん玉を作ることは可能でした。様子を見て調整してください。
ふたなどがあれば、数日間保存しておき、再度実験を行うことができます。
実験が終了したら食器洗いなどに使えば無駄がないと思います。
【立体図形をひたしてみよう!】
まずは、正四面体(正三角形が4面ある立体図形)から。

なるべく泡立たないように注意しましょう。
また、針金のフックなどがあると手が汚れず便利です。(フックは、針金でかんたんに作れます。)
正四面体の中にできたしゃぼん玉の膜をよく見てください。
面と面がきれいに120°に交わっています!
他の立体図形も試してみましょう!
次は、正六面体(サイコロ型)です。

正六面体の中にも120°で交わったしゃぼん玉の膜が見えます。

このようなふしぎな現象は、しゃぼん玉の膜に働く表面張力によるものです。
しゃぼん玉の膜には、表面積をできるだけ小さくしようとする力(表面張力)が働いています。
しかし、その力が強すぎてもしゃぼん玉は割れてしまいます。液体洗剤に含まれる界面活性剤は表面張力を弱める効果があるので、しゃぼん玉は割れにくいのです。
水の表面張力についてはこちらの記事を参考にしてみてください。
水の表面張力についての関連記事>>
美しい形のふしぎ~かがく好きになろう!
規則正しく美しい図形ができた時、そこには科学がひそんでいるかもしれません。
身の回りのふしぎをたくさん探してみましょう!
ふしぎ!本当?~算数や数学にふれてみよう!

しゃぼん玉の膜に表面張力が働いて、表面積をできるだけ小さくしようとしていることはわかったけど、なぜ120°なの?
こんな疑問はありませんか?
その疑問に答えるために、次のようなものを作ってみました。

①
プラスチック板を2枚、四角く切る。
②
目打ちのような尖ったものでそれぞれの板に4か所ずつ穴を開ける。1枚目と2枚目は同じ位置に穴を開ける必要があるので、2枚重ねて穴を開けてもOK。
③④
切ったモールを図のように穴に通して、2枚の板が平行になるようにモールの長さを調整する。余った部分はマスキングテープでとめる。
これをしゃぼん玉液につけて、取り出してみましょう。
注)なるべく泡立たないように静かに作業しましょう。
何度か繰り返していくうちに、こんな形が現れると思います。

見る角度を変えてみると・・・

見覚えのある形ですよね。
正六面体(サイコロ型)の中にできた形状です。

立体図形だとわかりにくいので、平面図形にして考えてみます。
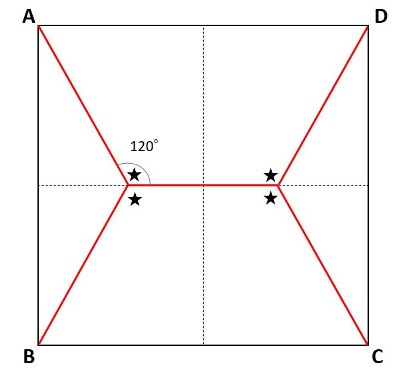
赤い線がしゃぼん玉の膜だと思ってください。
例えば、A、B、C、Dという4点を最短経路になるように結んだ線が、この赤い線です。赤い線同士が120°(図の★印の角度)で交わっていますね。

本当かどうか少しだけ確かめてみましょう。
今、□ABCDを正方形として考えてみると、正方形の中心からから左右対称になっているので、左側だけ、経路の合計距離を計算してみます。
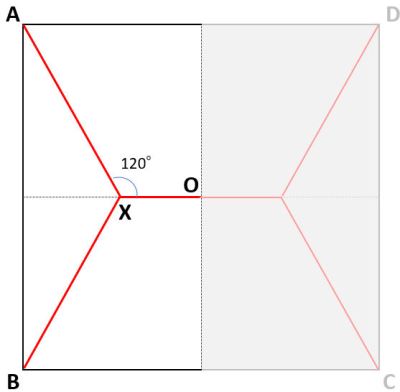
仮に一辺8cmの正方形とします。
【経路1:120°で交わる場合】
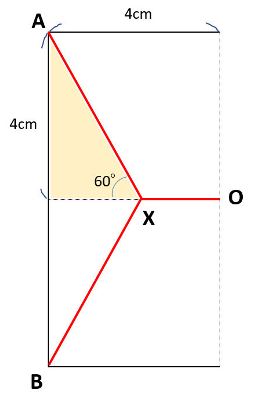
AX+BX+OXを求めてみましょう。およそ10.9cmになります。
三平方の定理がわかる方は、計算で。
わからない方は、方眼紙に作図して定規で測って求めても大丈夫です!
(120°の線を書く時は分度器よりも三角定規の60°の角を使うと書きやすいかもしれません。)

※ルートの計算は、関数電卓やエクセルなどを使用してください。
【経路2:A、B点から直接正方形の中心へ行く場合】
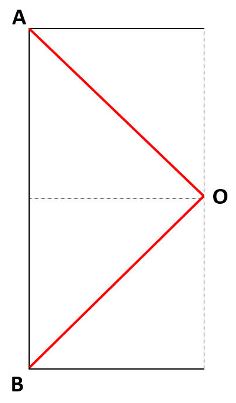
AO+BOはおよそ11.3cmになります。

あと2経路くらい試して確認しましょう。
【経路3:X点を右に移動した場合】
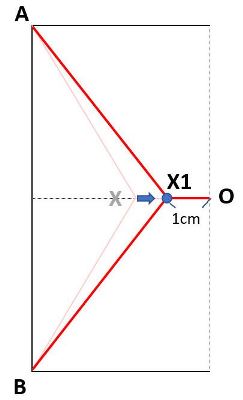
今、Xを右に移動した点をX1とし、X1とOの距離を1cmとします。
この時AX1+BX1+OX1は11cmになります。
【経路4:X点を左に移動した場合】
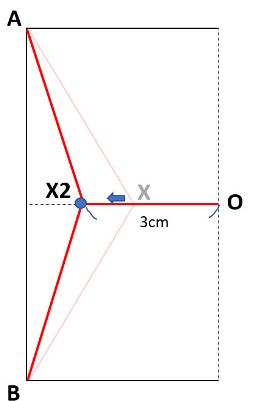
今、Xを左に移動した点をX2とし、X2とOの距離を3cmとします。
この時AX1+BX1+OX2は11.2cmになります。

この4つの経路を比較すると、経路1が一番短いことがわかりましたか?
赤い線が120°で交わる時が最短経路であることの完全な証明にはなりませんが、OとX2の間に最短距離になる点がありそうな感じが小学生でも何となくわかるのではないでしょうか。
さて、このような120°という角度は、自然界では結構登場します。
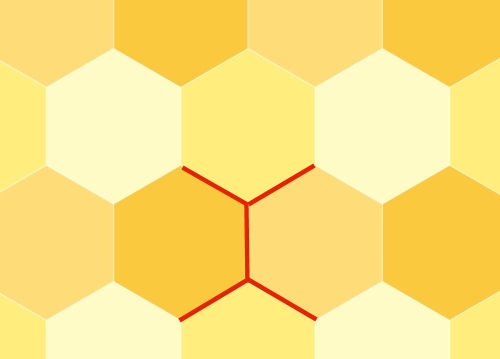
例えば上図に見覚えはありませんか?
このように正六角形を並べた形をハニカム構造といい、自然界ではハチの巣がまさにこの構造をしています。(正六角形の内角は全て120°です。)
ハチの巣がなぜこのような構造なのかという点については諸説ありますが、強度もありハチの巣の壁が最も少なくて済む形状だからと言われています。
ふしぎ!なぜ?~図形のふしぎを探そう!
しゃぼん玉の120°のお話をしてきましたが、自然界には内角が120°になる六角形の図形をしたものがハチの巣以外にも存在します。是非探してみてください!
例えば雪の結晶は、六角形を基本とした形をしています。

結晶はとてもきれいな形ものも多いので、原理などの難しいことはさておき、まずは図形として楽しんでみるのもお薦めです。
というのも、自然界における規則正しい美しい図形には、何かしらの科学が関与している可能性が高いからです。
例えば、ナスの漬物作りなどにも使われるミョウバンの結晶は、正八面体(正三角形が八面ある立体)です。

完璧な形の結晶を作るにはコツが必要で、私もまだ納得のいく結晶は作ることができません。(正八面体に近い結晶ができた時はちょっと感動ものです。)

ちなみに「ミョウバン」は、草木染めの媒染(発色や色止めのための処理)としても使われるので、興味があれば自宅でお子様と一緒に染めものも楽しんでみてください。玉ねぎの皮を使う玉ねぎ染めが染まりやすくてお薦めです。

玉ねぎの皮で染めた布をミョウバンに入れた途端、ぱっと色が変わって不思議なのです!
ミョウバンによる媒染も、草木の色素(フラボノイド)とミョウバンの金属イオンが反応するので、一種の科学実験です。
塩の結晶なら、基本的にはサイコロ型(正六面体)になります。

塩の結晶作りは家にあるものでできるので、自由研究などにもお薦めです。
作り方はこちらの記事を参照>>
ところで、実際に結晶作りをしてみるとわかりますが、塩の結晶にはこんな模様ができることも多いのです(下図)。

規則正しく模様がついていますよね?
赤線と青線はなぜできるのか?
2つの線は何度で交わっているのか?
気になったことを調べたり考えたりしてみてください!
正しい答えを出すことよりも、疑問に思って考えることが大切なのかなと思います。
水晶の結晶も六角柱を基本とした図形です。


自然にできる美しい図形を見つけて、その理由を考えてみると科学好きになれるかもしれません。
このように、例えば結晶の図形のふしぎなどに着目しながら、
- なぜそうなるの?
- 本当にそうなの?
- 自分でも確かめられるの?
- 正八面体、六角柱ってどんな図形なの?
同じ図形の結晶になる物質は他にあるのかな?
など、子供なりに考えていくことが科学の道への入口だと思います。そのために、「科学は楽しい!」と感じることが、実はとても大切なのかなと感じています。

結晶についていえば分子構造が関係しているので、科学の中でも特に中学や高校で習う化学に興味を持つきっかけにもなると思います。
化学に興味のあるお子様は、小学生の我が子がハマっている「空想科学学園」というマンガもお薦めです。
\固体・液体・気体における分子の状態なども楽しく学べます!/
結晶について、もっと知りたい小学生・中学生の方へ
※詳しい内容は、中学生~高校生で習うと思います。
【結晶について】
物質は、目に見えない粒の集まり(分子)でできています。
どんな粒が
どんな配置で
いくつ、どんな力によって集まっているのか
などは、物質によって決まっています。
例えば、水の分子はこんな感じです。
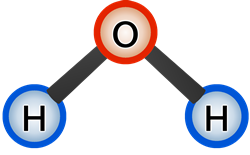
赤○1つからうでが2本のびて、その先に青○ついています。うでの角度も決まっています。
結晶にもいくつかの分類がありますが、結晶を大まかに言ってしまうと分子同士が規則正しく結合したものです。
だから、六角形や正八面体や正六面体などの美しい図形が現れることがあるというわけです。
自由研究にも~気になったことを追求してみよう!

連想ゲームのように、なぜ?なぜ?と自分が興味を持ったことをたどっていくと、おもしろい科学の自由研究になるかもしれません。
表面張力に興味を持ったら!
\表面張力の原理や簡単な実験の記事/

自然にできる図形の不思議に興味を持ったら!
\結晶づくりの定番!されど奥深い・・・!?/

気になったことを、どんどん調べてみましょう!


界面活性剤の性質(親水基、親油基など)についてもっと調べてみると。他にもおもしろい科学実験ができると思いますよ!
立派な自由研究を目指すよりも、科学が楽しいという気持ちを大切にしてみてくださいね!

