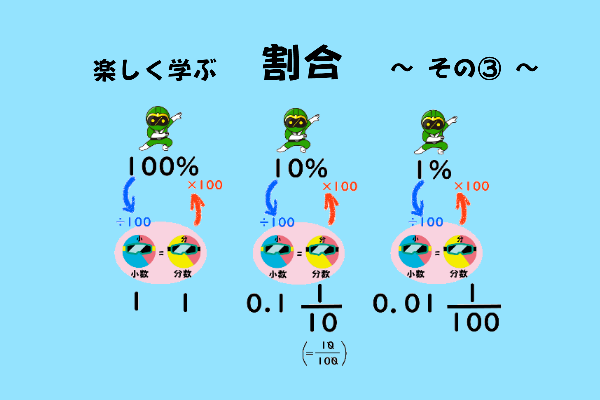
『割合』は、小学5年生・算数の中で苦手意識を感じている子供がとても多い分野です。
この割合について、苦手な子供でもわかりやすいようにイラストなどを使いながら楽しく苦手を克服する方法をお伝えしていきます。
例えば、半分を割合で表す方法は、いくつかあります。
小数で表すと・・・ 0.5
百分率で表すと・・・ 50%
分数だで表すと・・・ 1/2
これらの関係を理解してもらうことが、この記事の最終目標です。
今回は第三弾、『割合・その③~小数・分数・百分率の関係』について詳しく説明していきます。
1章:分数と小数~すがたを変えているだけです
まず、分数から見ていきましょう。
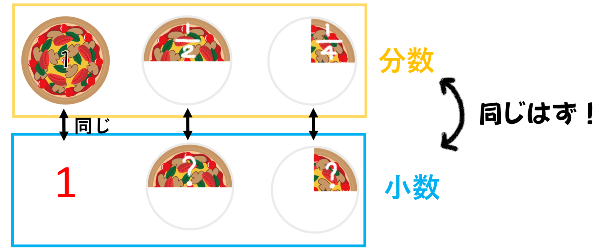
わかりやすいようにピザ1枚を1としてみましょう。
この時、1/2 と 1/4 はどうなるでしょうか?

上図のようになるとわかりましたか?
では小数の割合ではどうなるでしょうか?
前回(その②)、前々回(その①)の時に小数の割合について学習しましたよね。
小数の割合の時も、もとにする量を1とします。
今、ピザ1枚をもとにする量としていますので、小数の場合にもピザ1枚の割合が1になります。
もとにする量がどちらも1になるので、他の2つも分数と小数の割合は同じ大きさになるはずですよね。
つまり
1/2=1÷2=0.5
1/4=1÷4=0.25
・・・

分数の割合を小数になおす時は、分子÷分母をすればよいとわかります。
ただし、注意点がありますよ。

1/3のように1÷3=0.3333333・・・と割り切れない場合もあります。
そんな時は、分数のまま計算に使うことができます。
また、小数を四捨五入するなどして大まかな値になおしてから使うこともあります。
2章:百分率って何?~新キャラ登場!でも大丈夫です
小数・分数に続き、『百分率』という割合の新キャラが登場してしまいます・・・。
もとにする量を100とした割合のことで単位はパーセント(%)で表します。

パーセント→パーせんたい
ややこしそうに見えますが、大丈夫!
小数や分数の割合×100すれば『百分率』になってしまいますよ!
だから、逆に百分率を『小数や分数』の割合にする時は、百分率÷100となります。
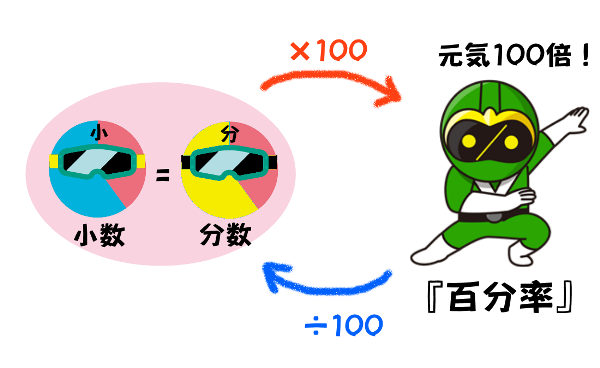
小数や分数のもとにする量:1
百分率のもとにする量:100
もとにする量が100倍になっているので、百分率は小数や分数の100倍になりますよ。
もう少しまとめてみましょう。
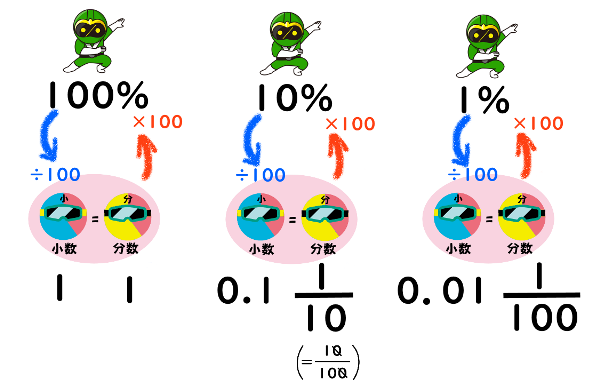
では、【練習問題】をといて具体的に見てみましょう。
◆◆◆練習問題①◆◆◆
0.75を百分率で表すと、何パーセントですか。
0.75を100倍すればいいのですよね。
だから、
0.75×100=75で、答えは75%になります。
◆◆◆練習問題②◆◆◆
22%を小数と分数で表しましょう。
22%を小数や分数になおすには、100で割ればいいのですよね。
だから、
22÷100=22/100=0.22

分数で答える時は約分しましょう。
22/100を約分すると11/50ですよね。
答え 分数:11/50、小数:0.22
3章:百分率は計算には使えないです
ちょっとだけ残念なお知らせです。
『百分率』は計算には使えません。

でも、大丈夫!
2章で学んだ通り、変身させればよいのです。
×100とか、÷100を覚えていますか?
これを理解できているかが、とても重要です。
【まとめ】ておきましょう。

- 計算で使う時は、小数(もしくは分数)になおして計算しましょう!
百分率÷100で、小数や分数に変身できます。
- 割合を百分率で答える問題の場合は、最後に百分率になおしましょう!
計算で出た小数(もしくは分数)の答えに×100すれば、百分率に変身できます。
ここで、ちょっとクイズです!
理解できたらすごい!!
※難しいなと思う方はとばして次の章へ!


解き方は1つではありません。
ここでは0.555を例にとって、2つの解き方を紹介します。
どちらの解き方がわかりやすいかな?
解き方①
ステップ1:何らかの分数に変形する
0.555=0.555/1 という分数に変形します。
ステップ2:小数が残っていたら整数になおす
分子の小数を整数になおしたいな・・・。
こんな時は約分の考え方を思い出してください。
【分数の性質】
分子と分母それぞれに同じ数をかけても分数の大きさは同じ。
逆に、分子と分母それぞれを同じ数で割っても分数の大きさは同じ。
だから、
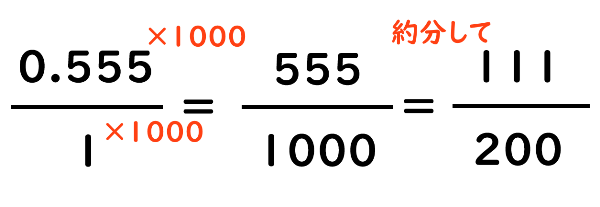
となり、答えは111/200となります。
解き方②
ステップ1:何らかの分数に変形する
0.555は100倍すれば百分率になりますね。
だから、
0.555×100=55.5 で55.5%になります。
百分率を100で割れば分数になりますから、
55.5/100という分数に変形することができます。
ステップ2:小数が残っていたら整数になおす
まだ分子に小数が残っていますから、これを整数になおしましょう。
ここでもまた、約分の考え方です。
【分数の性質】
分子と分母それぞれに同じ数をかけても分数の大きさは同じ。
逆に、分子と分母それぞれを同じ数で割っても分数の大きさは同じ。
だから、

となり、答えは111/200となります。
4章:文章題(百分率)のコツ~たったこれだけです

安心してください。
割合の文章題の解き方は、小数(もしくは分数)でも百分率でも、実はほとんど変わりません。
ですから、基本的な解き方は前回(その②)と前々回(その①)の記事に掲載した数直線を使った解き方を参考にしてくださいね。


ただし、百分率は計算には使えませんので、変身させてあげる必要があります。
変身こそが、百分率が出てくる文章題のコツです!

例① 『割合』を百分率で求める時
まず、割合を小数(もしくは分数)で求める。
↓
計算で求まった答えに×100をして百分率の『割合』に変身させる。
例② 百分率の割合で出題され、そこから『比べる量』や『もとにする量』を求める時
百分率の割合は計算に使えないので、÷100をして小数(もしくは分数)に変身させる。
↓
小数(もしくは分数)の割合を使って計算をし、『比べる量』や『もとにする量』を求める。

1章~4章までの内容を頭に入れて、学校の教科書やドリルを解いてみてください!
練習問題を解くことで、少しずつ身についていくと思いますよ。
5章:算数が苦手な子供への具体的な対処法
苦手分野が何かと多い小学生の息子と家庭学習する中で、私が必要だと感じた対処法は次の通りです。
算数が苦手な子供への具体的な対処法
- ステップ バイ ステップで!
確認とまとめを繰り返しながら、少しずつ教える。
- イラストや色の活用
覚えにくいことはイラストに置き換えてみたり、赤や青など2~3色の色を使って色分けしながら教える。
- ある程度の『型』を覚える
丸暗記にならないよう、ちゃんと意味も考えさせるように工夫する。
- 算数嫌いにならない工夫
子供の好みに合わせて、楽しませる工夫をする。
我が家の例)
ばかばかしくて笑えることが好きな息子と、算数のオリジナルキャラクターを考える。
【参考情報】
『すらら』という通信教材は、算数の苦手克服にとても適していると思います。我が子の反応などは無料体験記事を参考になさってください。

※無料体験の中に『割合』の単元は無かったと思いますが、無学年式なので何年生の単元でも体験することができます。